Osnova:
Co je to umocňování?
Umocňování je matematická funkce, která vyjadřuje opakované násobení. Umocňování je k násobení v podobném vztahu jako násobení k sčítání. Slouží ke zkrácenému zápisu vícenásobného násobení:
$\Large \underbrace{z \cdot z \cdot z \cdot z \cdots}_{n \operatorname{-kr\acute{a}t}} = z^n$
V tomto vzorci je $z$ jako základ mocniny (mocněnec) a $n$ se nazývá exponent nebo mocnina (mocnitel). Celý vzorec $z^n$ se pak čte „n-tá mocnina čísla z“ nebo „z na n-tou“. Příklad:
$10^2$ je „deset na druhou“ nebo „druhá mocnina čísla deset“
Vlastnosti mocnin
- $z^{−n} = \frac{1}{z^n}$
- $z^{\frac{m}{n}}=\sqrt[n]{z^m}$
- $z^0 = 0, \text{ pokud } z \neq 0$
- $a^1 = a$
- $0^n = 0, \text{ pokud } n > 0$
- $0^0 \text{ je obecně nedefinováno}$
- $(a \cdot b)^n = a^n \cdot b^n$
- $a^n \cdot a^m = a^{n+m}$
- $\frac{a^n}{a^m} = a^{n-m}$
- $(a^n)^m = a^{n \cdot m}$
Vědecká notace
Vědecká notace nebo také vědecký zápis čísel je způsob reprezentace hodně vysokých a nízkých čísel. Zapisuje se ve dvou tvarech:
$\large a \text{E}b$
nebo
$\large a \cdot 10^b$
$a$ je desetinné číslo které se nazývá mantisa a $b$ je celé číslo, které je nazývané charakteristika čísla, nebo exponent. Příklad:
$1.25\text{E}10 = 12 500 000 000$
$9.32\text{E}-12= 0.00000000000932$
$5.4297 \cdot 10^{8} = 542 970 000$
$7.1 \cdot 10^{-9} = 7.1 \cdot \frac{1}{10^9} = 0.0000000071$
Pravidla zápisu
Mantisa je číslo v rozmezí od 1 (včetně) do 10 (vyjma), exponent rozsahem omezený není. Exponent umocňuje číslo 10, protože je to základ běžně užívané desítkové soustavy. Tím pádem to posouvá desetinou čárku. Kdyby jste počítali s jinou soustavou tak použijete jiné číslo. Mantisa i exponent mohou být jak kladná tak i záporná. Záporná mantisa znamená že číslo je menší než 0. Záporný exponent znamená že číslo leží v otevřeném intervalu (-1, 1). A kladný exponent znamená že číslo je větší než 10.
Odmocniny
Odmocnina je inverzní funkce k mocnině. Nejčastěji se pracuje s druhou mocninou, která hledá takové číslo, které když vynásobíme se sebou samým, tak získáme původní číslo, které jsme odmocnili.
Pro odmocninu se používá znak $\Large \sqrt{}$. Druhá odmocnina se značí jen $\Large \sqrt{}$ a každá vyšší se značí už $\Large \sqrt[n]{}$, kde $\Large n$ je počet kolikrát musíme samo sebou vynásobit to číslo, které hledáme, aby jsme dostali to které chceme odmocnit.
$\Large \sqrt[n]{a}=b\Leftrightarrow b^n=a$
V tomto článku budeme pracovat s tím že $n \in \mathbb{N}$ a $a,b \in \mathbb{R}$
odmocnina ze záporného čísla
Všechny sudé vícenásobné mocniny odmocniny jako $\sqrt[2]{}$, $\sqrt[4]{}$ atd. nemůžou odmocnit záporné číslo. Proč je tomu tak?
Když zkusíme umocnit jakékoli číslo sudým mocnitelem tak nám vždy vyjde kladné číslo. Příklad:
$(-4)^2 = (-4)\cdot(-4) = 16$
$4^2 = 4\cdot4 = 16$
$6^2 = 6\cdot6 = 36$
Naopak u lichých mocnitelů už záporné číslo získat můžeme:
$(-4)^3 = (-4)\cdot(-4)\cdot(-4) = -64$
$(-2)^5 = (-2)\cdot(-2)\cdot(-2)\cdot(-2)\cdot(-2) = -32$
Vzorce pro odmocniny
Jak převest mocninu na odmocninu jste mohli vidět výše, pro zopakování zde je to ještě jednou, a k tomu, nějaké vzorce přímo pro odmocniny.
- $\sqrt[n]{a^m}=a^{\frac{m}{n}}$
- $\sqrt[n]{a\cdot b}=\sqrt[n]{a}\cdot\sqrt[n]{b}\qquad a,b\ge0$
- $\sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}\qquad a,b\ge0$
- $\sqrt[n]{\sqrt[m]{a}}=\sqrt[n\cdot m]{a}$
- $\sqrt[n]{0}=0$
- $\sqrt[n]{1}=1$
- $\sqrt[1]{a}=a$
Co jsou to tetrace?
Podobně jak opakované násobeni tetrace jsou opakované umocňovaní:
$\Large {}^na = \underbrace{a^{a^{\cdot^{\cdot^{a}}}}}_{n}$
Zatím to moc využití nemá, protože rychle dostanete hodně vysoké čísla. Jako například zde jsou tetrace čísla tři:
${}^1 3 = 3$
${}^2 3 = 3^3 = 27$
${}^3 3 = 3^{3^3} = 7 625 597 484 987$
${}^4 3 = 3^{3^{3^3}} = 3^{7 625 597 484 987}$
Tetrace sice zatím nemají pořádné využití, ale vyvaří zajimavé grafy:
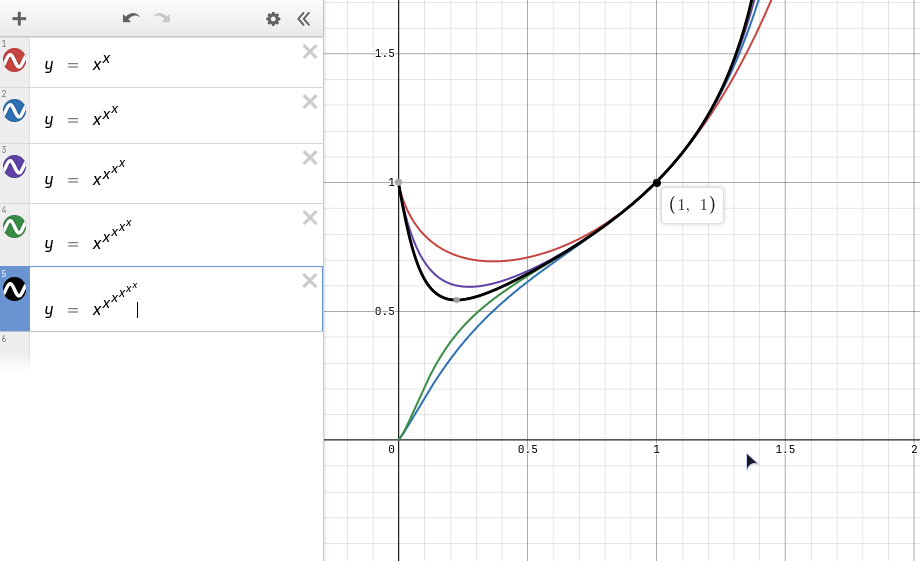
Zde někdo vytvořil fraktály pomocí tetrací:

Samozřejmě k tetracím existují i další funkce jako „Super-root“ česky „Super-odmocnina“, nebo „Super-Logaritmus“.
Můžeme pokračovat i dál. Třeba pentace je opakovaní tetrace, hexace je opakovaní pentace atd.
Můžeme jít do nekonečna. Proto se místo názvů jako tetrace, pentace atd. používá hyper a číslo. Začínáme u sčítání což je „hyper-1“. Pak je „hyper-2“ násobení a takhle jdeme dál. Jak možná tušíte tak tetrace bude „hyper-4“, pentace „hyper-5“ atd.


Napsat komentář