Osnova:
Budeme zde počítat jen s 2D vektory. 3D vektory nejsou o moc jiné, ale rozeberu je podrobněji v budoucnu.
No než se vrhneme na vektory musíme si vysvětlit co to je orientovaná úsečka.
Orientovaná úsečka:
Máme dva různé body A, B. Mezi těmito body muže vést úsečka. Takovou úsečku obvykle zapisujeme jako AB, zároveň platí že nezaleží na pořadí bodů. Úsečka AB je uplně stejná jako úsečka BA
To se nám občas nehodí a proto zavádíme pojem orientovaná úsečka, u které rozlišujeme počáteční bod a koncový bod. Orientovaná úsečka AB má počáteční bod A a koncový B. Na obrázku značíme orientovanou úsečku šipkou a v textu zapisujeme pomocí šipky nad body: $\overrightarrow{AB}$.
Velikost orientované úsečky je stejná jako velikost normální úsečky. Platí $|\overrightarrow{AB}|=|AB|$
Co je to vektor?:
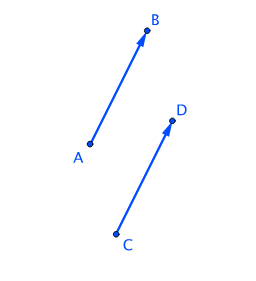
Jediný rozdíl mezi těmito úsečkami je, že jsou umístěné někde jinde. Takové orientované úsečky, které mají stejný směr a stejnou velikost představují ten stejný vektor.
Vektory obyčejně zapisujeme tučně a s šipkou stejně jako orientovanou úsečku. Můžeme tak mít vektor $\overrightarrow{AB}$ nebo zkráceněji vektor $\overrightarrow{v}$.
Vektor je daný pouze svou velikostí a směrem. Následující orientované úsečky tak všechny představují jeden vektor:
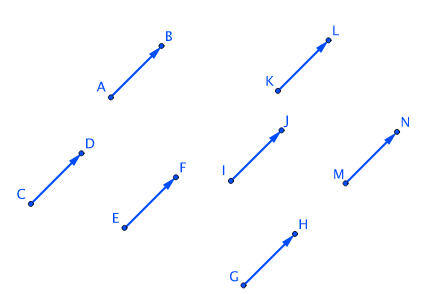
Jak se počítá s vektory?:
Opačný vektor:
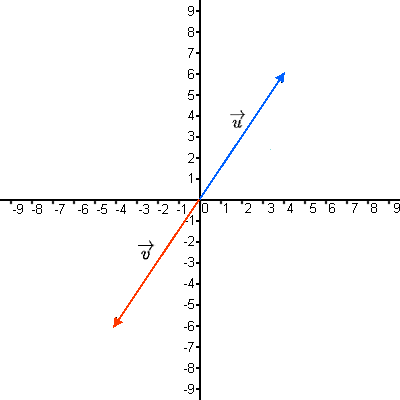
Na obrázku vidíme dva vektory. $\overrightarrow{u} = (4,6)$ a $\overrightarrow{v} = (-4,-6)$.
Můžeme říct že opačný vektor $\overrightarrow{v}$ tedy $-\overrightarrow{v}$ je roven vektoru $\overrightarrow{u}$
V podstatě souřadnice vektoru vynásobíme $-1$:
$-\overrightarrow{v} = (-4\cdot-1, -6\cdot-1) = (4, 6)$
Sčítání a odčítání vektorů:
Pokud máte dva vektory jako např. $\overrightarrow{u} = (u_{1}, u_{2})$ a $\overrightarrow{v} = (v_{1}, v_{2})$ pak jejich součet je roven:
$\overrightarrow{u} + \overrightarrow{v} = (u_{1}+v_{1}, u_{2}+v_{2})$
Pokud bychom dosadili čísla do vektorů. $\overrightarrow{u} = (5, 8)$ a $\overrightarrow{v} = (3, 1)$ tak by to vypadalo takto:
$\overrightarrow{u} + \overrightarrow{v} = (5+3, 8+1) = (8, 9)$
Pokud odčítáte vektory, je to stejné, jako byste přičítali opačný vektor:
$\overrightarrow{u} – \overrightarrow{v} = (u_{1}-v_{1}, u_{2}-v_{2})$
Násobení vektorů číslem:
Vektor můžeme vynásobit nějakým číslem ale i druhým vektorem. Násobení vektorů mezi sebou si vysvětlíme příště. Vektory nemůžeme dělit mezi sebou, ale dají se dělit reálným číslem.
Máme např. vektor $\overrightarrow{v} = (v_{1}, v_{2})$. Pokud bychom ho chtěli vynásobit např. dvakrát tak to bude vypadat následovně:
$2\overrightarrow{v} = (2\cdot v_{1}, 2\cdot v_{2})$
Příklad s čísly:
$\overrightarrow{v} = (12, 43)$
$4\overrightarrow{v} = (4\cdot 12, 4\cdot 43) = (48, 172)$
vyjadřední velikosti vektoru pomocí jeho souřadnic:
Velikost $|\overrightarrow{v}|$ vektoru $\overrightarrow{v}$ vyjádříme jednoduše pomocí Pythagorovy věty.
$|\overrightarrow{v}| = \sqrt{v_{1}^2 + v_{2}^2}$
Co je to skalár?:
Skalár ve fyzice, v matematice nebo informatice je veličina hodnota která je plně určena jediným číselným údajem. Protikladem skalární veličiny jsou vektory nebo tenzory, které jsou určeny více číselnými hodnotami. Například fyzikální veličina hmotnost je skalár a síla je vektor – má velikost a směr.
Zdroje:
Operace s vektory – Tomaš Chabada – Youtube
Operace s vektory – Matematika polopatě
Knihy:
- Přehled středoškolské matematiky – Josef Polák

