Osnova:
Základní množinové pojmy
Množina je souhrn předmětů (prvků), které jsou jasně určené. Množiny se zpravidla označují velkými písmeny a jejich prvky malými. Můžeme udělat seznam plemen koček. Množina plemen koček se může jmenovat třeba $P$. Můžeme říct že Britská krátkosrstá kočka náleží množině $P$, nebo třeba Britská krátkosrstá kočka je z množiny $P$. V matematice používáme symbol $∈$. Takže v matematickém zápisu to bude vypadat následovně.
Britská krátkosrstá kočka $∈ P$
Taky můžeme říct že tam něco nepatří, to vyjádříme symbolem $\notin$. Ten se čte jako „není z množiny“ nebo „není prvkem množiny“.
Shiba inu $\notin P$1
Množiny dělíme na dva typy podle počtu prvků:
- konečné množiny – taková množina které má konečný počet prvků, třeba jako naše množina koček
- nekonečné množiny – tam je nekonečno prvků, třeba jako množina všech celých nebo všech záporných čísel.
Zápis množin:
- Zápis výčtem prvků – do složené závorky napíšeme všechny prvky (například čísla), která daná množina obsahuje. Většinou jsou čísla seřazená vzestupně, od nejmenšího po největší. Dále si zvolíme libovolně zvolíte název množiny. Tento zápis je možný pouze pro konečné množiny.
$A = \{ 1; 5; 45; 75; 153\} $
$Z = \{ a; h; p; y\} $ - Zápis charakteristickou vlastností – můžeme ho použít pouze tehdy, když prvky v množině mají nějakou charakteristickou vlastnost. Libovolně si zvolíme název, napíšeme $=$ a pak do složených závorek napíšeme něco jako {neznámá ∈ množina ze které pochází neznámá; vlastnost}. Neznámou si libovolně zvolíme nebo její název je v zadání, množina ze které pochází je většinou daný číselný obor a pak je tam ta charakteristická vlastnost.
$A = \{ x ∈ \mathbb{N}; x < 5\} $
$Z = \{ m ∈ \mathbb{R}; m > 21\} $ - Grafické znázornění – Obvykle základní množina Z sa znázorňuje obdelníkem a její podmnožiny většinou A a B jako kruhy nebo jiné většinou oválné obrazce vevnitř obdelníku. Těm se říká Vennovy diagramy. K znázornění množin reálných čísel se obvykle používají číselné osy. O Vennových diagramech ještě budu psát dále a o znázornění na ose se zmíním u intervalů.
Rovnost množin:
Rovnost množina $A$ a $B$ nastává pokud jsou všechny prvky v množině $A$ stejné jako v množině $B$.
$A = B$
Podmnožiny:
Pokud všechny prvky z množiny B jsou i v množině A, pak můžeme říct že množina B je podmnožinou množiny A nebo že nastává inkluze. Zápis vypadá takhle:
$B\subset A$
Pokud máme množinu všech koček který nám běhají na zahradě tak je zároveň podmnožinou množiny všech koček na zemi.
Kočky na zahradě $\subset$ Kočky
Prázdné množiny:
Prázdné množiny se zapisují pomocí symbolu $\emptyset$ nebo jako prázdné závorky2.
$A = \emptyset$
$A = \{ \}$
Vennovy diagramy
Vennovy diagramy vypadají asi nějak takhle:
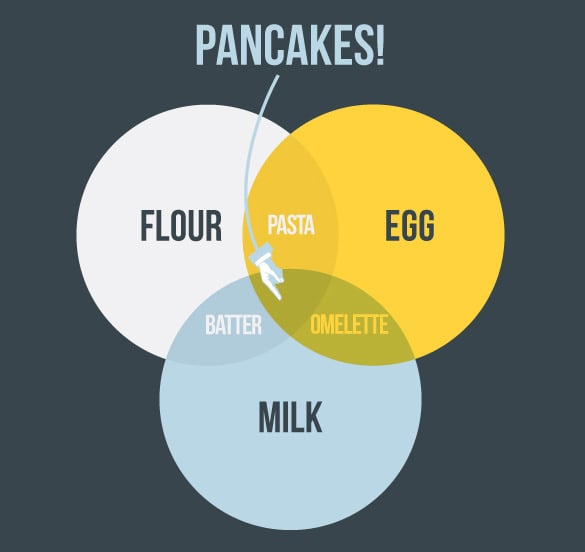

Vennovy diagramy jsou v podstatě schématické nákresy množin. Pomocí nich můžeš řešit složitější příklady ve kterých je potřeba přehlednost. Zde jsou nějaké další příklady Vennových diagramů:
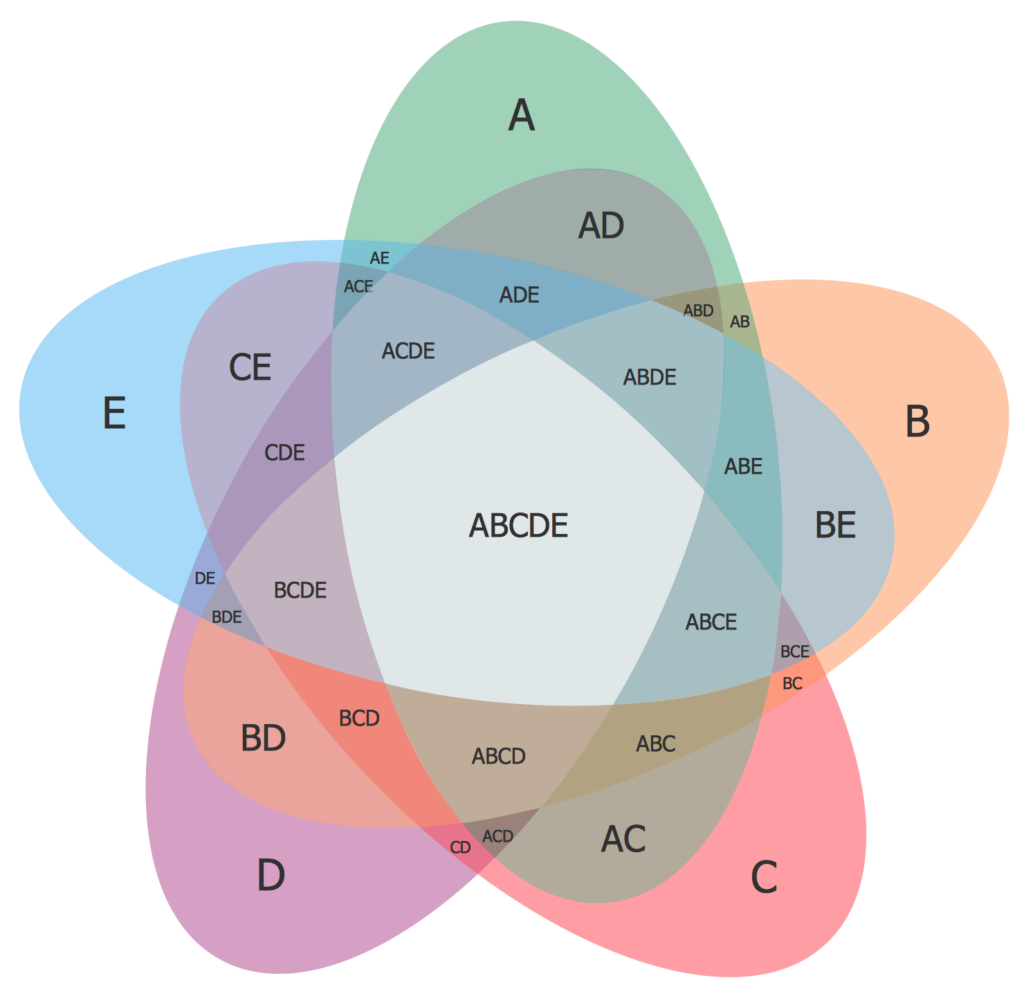
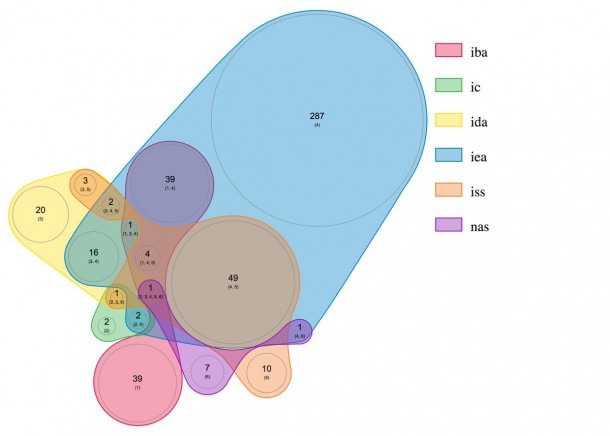

Operace s množinami
Mějme danou základní množinu $U$ a prvky všech dalších uvažovaných množin v této části3 budeme brát z ní.
Sjednocení

V podstatě se spojí obě množiny do jedné a vznikne množina kde se nachzí prvky které byly alespoň v jedné z původních množin.
průnik
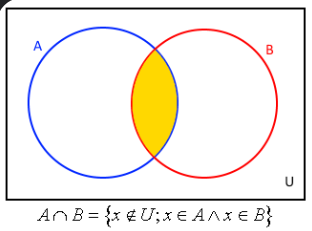
Průnik množin A a B je množina všech prvků které se nacházejí v obou množinách.
rozdíl
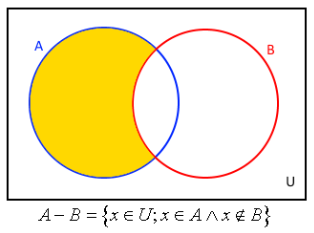
Rozdílem množin $A$ a $B$ vnikne nová množina obsahující všechny prvky které jsou v množině $A$ a zároveň nepatří do množiny $B$.
doplněk
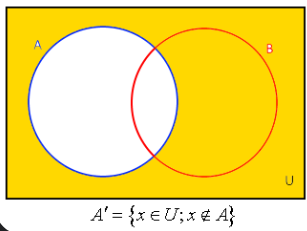
Pokud je množina $A$ podmnožinou množiny $B$ tak můžeme udělat doplněk. Doplněk množiny $A$ v množině $U$ obsahuje takové prvky které nejsou v množině $A$ a zároveň jsou v množině $U$.
Intervaly
Interval je podle definice podmnožina množiny všech reálných čísel, která je z obou stran ohraničena dvěma krajními body. Krajní bod může být i nekonečno.
typy intervalů
Interval omezený:
Takový interval, který je omezený z obou stran přesnými hodnotami, nikoli nekonečnem. 45
| Zápis intervalu | Charakteristická vlastnost | |
| Uzavřený interval | $ \langle a; b\rangle $ | $a \leq x \leq b; x\in \mathbb{R}$ |
| Polouzavřený interval zprava | $(a; b\rangle $ | $a < x \leq b; x\in \mathbb{R}$ |
| Polouzavřený interval zleva | $ \langle a; b)$ | $a \leq x < b; x\in \mathbb{R}$ |
| Otevřený interval | $(a; b)$ | $a < x < b; x\in \mathbb{R}$ |
Interval neomezený:
Je interval který je omezený přesnou hodnotou maximálně z jedné strany.6
| Název | Zápis intervalu | Charakteristická vlastnost |
| Interval neomezený zprava a uzavřený zleva | $\langle a; ∞)$ | $x \geq a; x\in \mathbb{R}$ |
| Interval neomezený zprava a otevřený zleva | $(a; ∞)$ | $x > a; x\in \mathbb{R}$ |
| Interval neomezený zleva a uzavřený zprava | $(-∞; a\rangle $ | $x \leq a; x\in \mathbb{R}$ |
| Interval neomezený zleva a otevřený zprava | $(-∞; a)$ | $x < a; x\in \mathbb{R}$ |
| Interval neomezený z obou stran | $(-∞; ∞)$ | $-∞ < x < ∞; x\in \mathbb{R}$ |
Jak zapsat interval
Dva krajní body v závorkách:
Do závorek napíšeme dva body, první menší a druhý větší7. Pak je oddělíme středníkem8. Dále záleží na typu závorek. Pokud je tam závorka „(“ nebo „)“, znamená to že krajní bod do intervalu nepatří. Pokud je tam „$\langle $“ nebo „$\rangle $“ znamená to že krajní bod do intervalu patří.
Charakteristická vlastnost:
Tenhle způsob se většinou používá u zápisu množin. Prvně se zapíše menší krajní bod a potom znaménko nerovnosti (< nebo $\leq$). Dále napíšeš neznámou (většinou x ale je to jedno) a zase znaménko nerovnosti. Nakonec přijde větší hodnota.
Grafické znazornění na ose:
Vypadá tak že máme časovou osu a na ní to graficky vidíme. Tento způsob se hodí spíše když si potřebujeme představit více intervalů najdenou aby jsme viděli co mají společné.
| Název intervalu | Dva krajní body v závorkách | Charakteristická vlastnost | Znázornění na ose |
| uzavřený interval a, b | $ \langle a; b\rangle $ | $\{ a \leq x \leq b; x\in \mathbb{R}\}$ | |
| polouzavřený interval a, b (zleva otevřený a zprava uzavřený) | $(a; b\rangle $ | $\{ a < x \leq b; x\in \mathbb{R}\}$ | |
| polouzavřený interval a, b (zleva uzavřený a zprava otevřený) | $ \langle a; b)$ | $\{ a \leq x < b; x\in \mathbb{R}\}$ | |
| otevřený interval a, b | $(a; b)$ | $\{ a < x < b; x\in \mathbb{R}\}$ |  |
Operace s intervaly
Průnik intervalů:
Průnik intervalů $a$ a $b$ je interval (množina) prvků které mají intervaly $a$ a $B$ společné. Dobře se to dělá na ose s grafickým znázorněním.
Sjednocení intervalů:
To je docela jednoduché, pokud máme intervaly $a$ a $b$ tak sjednocením těchto dvou intervalů vznikne nový interval ve kterém jsou prvky které jsou alespoň v jednom z původních intervalů.

Napsat komentář