Logaritmy

• Co je to Logaritmus?
• Další logaritmické funkce
  • Přirozený logaritmus
  • Dekadický logaritmus
• Vlastnosti logaritmu
• Grafy
  • Proč grafy prochází bodem [1, 0] a [0, 1]?
• Vzorce a vztahy
• Jak pomocí logaritmu vyjádřit jiný logaritmus

Logaritmus je matematická funkce, která se ptá: „Jakým číslem musím umocnit $a$ abych dostal $x$?“. Je tedy inverzní k mocninám neboli exponenciální funkci.

Zapisujeme slovem $\log$, a $\ln$ pokud se jedná o přirozený logaritmus (viz dále). Tento zápis čteme následovně: „Logaritmus čísla $x$ o zakladu $a$ je roven $y$“.

$\log_a{x} = y$

Zde můžeme vidět jak mezi sebou souvisí exponenciální a logaritmická funkce:

$\log{\color{Maroon}{_a}{\color{MidnightBlue}{x}}} = {\color{LimeGreen}{y}} \Leftrightarrow {\color{Maroon}{a}}{\color{LimeGreen}{^y}} = {\color{MidnightBlue}{x}}$

Přirozený logaritmus:

Jako základ má Eulerovo číslo, které značíme $e$.

Eulerovo číslo je iracionální, tedy s nekonečným desetinným rozvojem. Jeho přibližná hodnota je: $e = 2.718281$

Přirozený logaritmus zapisujeme buď jako $\log_e{x}$ nebo jednodušeji jako $\ln{x}$. Písmeno „n“ je tam z latinského „logaritmus naturalis“, ale na zapamatování postačí angličtina kde je to velmi podobné: „naturalis“ = „natural“ = „přirozený“.

Dekadický logaritmus:

Je to logaritmus o zakladu $10$. Můžeme jej zapsat obyčejně $\log_{10}{x}$ nebo zkráceně jen jako $\log{x}$. Tedy pokud u logaritmu není uveden základ, předpokládá se že je základ $10$.

Jak víme, logaritmická funkce je inverzní k exponenciální. Díky tomu také přebírá některé její vlastnosti a omezení. Takže základ musí být reálné číslo které je větší než nula a různé od jedničky. Zápis logaritmické funkce:

$y=\log_ax,\quad a\in\mathbb{R},\quad a>0,\quad a\ne1$

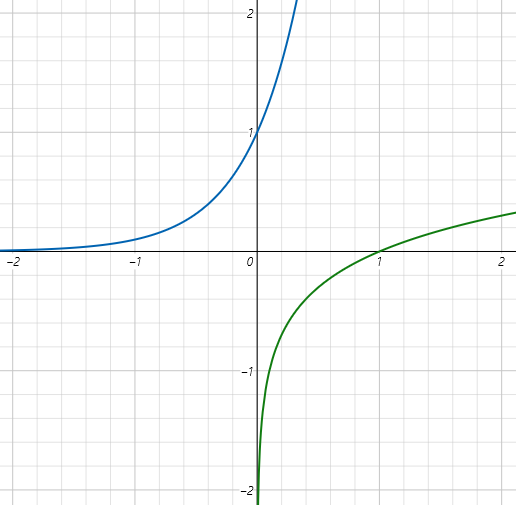
Modrý graf je exponenciální funkce a ji inverzní logaritmická funkce je zelená.

Proč grafy prochází bodem [1, 0] a [0, 1]?:

Každá exponenciální funkce prochází bodem [0, 1]. Logaritmus je inverzní funkce, tak tato funkce musí vždy procházet bodem [1, 0].

Takže hledáme exponent, kterým když umocníme zaklad tak dostaneme jedničku. Což je nula. Ať je zaklad jakýkoli tak na nultou se bude vždy rovnat jedna. Logaritmus bude obráceně, což už jsem vysvětlil o odstavec výše.

Předpokládejme že pro základ $a$ opravdu platí že $a>0$, $a \neq 1$. A také $x_1$ a $x_2$ budou libovolná reálná čísla. Poté platí že:

$\log_a{(x_1 \cdot x_2)} = \log_a{x_1} + \log_a{x_2}$

$\log_a{(\frac{x_1}{x_2})} = \log_a{x_1} – \log_a{x_2}$

$\log_a{x^r} = r \cdot \log_a{x}$ $\forall r \in \mathbb{R}$

$\log_a{\sqrt[n]{x}} = \frac{1}{n} \log_a{x}$ $\forall n \in \mathbb{N}$

Některé vztahy vyplívají přímo z definice logaritmu:

$\log_a{1} = 0$ $(a^0=1)$

$\log_a{a}=1$ $(a^1=a)$

$a^{\log_a{x}}=\log_a{a^x} = x$

Občas se stane, že v kalkulačce máme k dispozici jen logaritmus přirozený a dekadický. Ale co dělat když potřebujeme vypočítat logaritmus o jiném zakladu? Existuje vzorec ve kterém platí že:

$\log_a{x}=\frac{\log_b{x}}{\log_b{a}}$

Pokud za hodnotu $b$ dosadíme Eulerovo číslo, získáme tím vzorec:

$\log_a{x} = \frac{\ln{x}}{\ln{a}}$

Kdyby jsme například chtěli spočítat logaritmus čísla 8 o zakladu 2. Budeme ho počítat takto:

$\log_2{8} = \frac{\ln{8}}{\ln{2}} = 3$

Nebo můžeme použít jakýkoli jiný základ místo $b$.

Khan Academy – Co je to logaritmus?

Matematika polopatě – Logaritmy