Osnova:
Úvod:
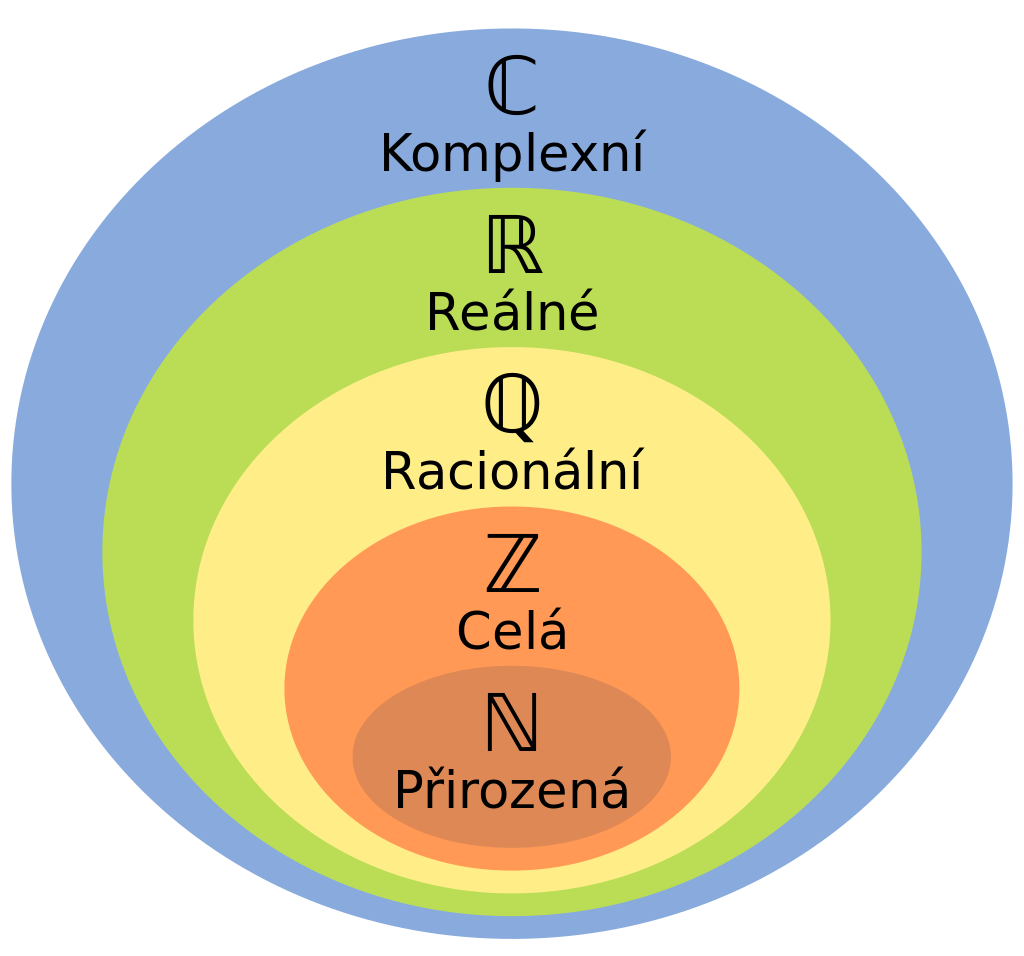
Zde jsou druhy čísel které známe
| Přirozená čísla $1, 2, 3, 4, 5,$ … |
Vyjadřuje počet | Značí se buď N nebo zdvojeným písmenem $\mathbb{N}$ |
| Celá čísla $-5, -2, 0, 4, 80,$ … |
Vyjadřuje změny v počtu a obsahují všechna přirozená čísla | Značí se Z nebo $\mathbb{Z}$ |
| Racionalní čísla $68.24, -9, 3.58, 6.\overline{6}, \frac{22}{7}, $ … |
Všechna čísla která jdou zapsat na konečný počet desetiných míst. Obsahují všechna celá čísla | Značí se Q nebo $\mathbb{Q}$ |
| Iracionalní čísla $\pi, e, \sqrt{2},\sqrt{3},\varphi,$ … |
Všechna čísla která mají nekonečný počet desetiných míst, nejdou zapsat pomocí zlomku a nejsou periodická. | Neznačí se |
| Reálná čísla $3 ,-4\pi, 6.\overline{6}, -9, 68.24, \frac{4}{7}, $ … |
Obsahují všechna racionalní a iracionalní čísla | Značí se R nebo $\mathbb{R}$ |
| Komplexní čísla $\sqrt{-1} $ … |
Obsahují čísla která dostaneme pokud např. odmocníme negativní číslo a také obsahují všechna reálná čísla | Značí se C nebo $\mathbb{C}$ |
Přirozená čísla:
- Přirozená čísla je množina která obsahuje kladná celá čísla, tedy $1, 2, 3, 4, 5,$ …
- Jsou to nejčastější čísla se kterýmy se setkáváme v běžném životě
- Jsou nekonečná spočetná množina čísel
- Základní operace s přirozenými čísly jsou sčítání a násobení
- Tuto množinu obvykle značíme pomocí písmene N se zdvojenou první nožkou, takto: $\mathbb{N}$
Občas předpokládáme, že množina přirozených čísel obsahuje i nulu. Pokud to potřebujeme rozlišit, používáme $\mathbb{N}$ pro množinu bez nuly, nebo když to chceme zvýraznit tak přidáme plus $\mathbb {N}^+$. Pokud chceme počitat i s nulou, pak přidáme nulu do indexu takto: $\mathbb{N}_0$.
Přirozená čísla používáme také pro určování množství např. „Máme tři bombóny“, „V parku je padesát kachen“, atd. a pro určení pořadí „První člověk na Marsu“, „To je desátý meteor co jsem dnes viděl!“, atd.
| Pro každá přirozená čísla (v tomhle připadě $a, b, c$) platí: |
| Součet $𝑎 + 𝑏$ je přirozené číslo. | Součin $𝑎 \cdot 𝑏$ je přirozené číslo. | U |
| $𝑎 + (𝑏 + 𝑐) = (𝑎 + 𝑏) + 𝑐$ | $𝑎 \cdot (𝑏 \cdot 𝑐) = (𝑎 \cdot 𝑏) \cdot 𝑐$ | A |
| $𝑎 + 𝑏 = 𝑏 + 𝑎$ | $𝑎 \cdot 𝑏 = 𝑏 \cdot 𝑎$ | K |
| $1 \cdot 𝑎 = 𝑎$ | N | |
| $𝑎(𝑏 + 𝑐) = 𝑎𝑏 + 𝑎𝑐$ | D |
| U | Uzavřenost | Součtem i součinem libovolných přirozených čísel je vždy přirozené číslo |
| A | Asociativnost | Sčítance při součtu, resp. činitele při násobení můžeme libovolně sdružovat |
| K | Komutativnost | Pořadí sčítanců při součtu, resp. pořadí činitelů při násobení můžeme zaměnit |
| N | Neutrálnost | Číslo 1 je neutrálním prvkem vzhledem k operaci násobení |
| D | distributivnost | násobíme-li číslem součet dvou nebo více čísel, vynásobíme tímto číslem každého sčítance |
Celá čísla:
- Tuto množinu značíme pomocí písmene Z nebo $\mathbb{Z}$
- Celá čísla na rozdíl od přirozených obsahují i záporná čísla
- Jsou nekonečná spočetná množina čísel
- Základní operace s celými čísly jsou sčítání a násobení jako u přirozených čísel a také odčítání
- Ke každému celému číslu existuje inverzní číslo. Např. inverzní číslo $10$ je $-10$ nebo třeba inverzní číslo $-98$ je $98$
Sudá a lichá čísla:
Celá čísla mužeme dělit na sudá a lichá čísla. Sudá čísla jsou ta, která jsou dělitelná dvojkou jako $-20, -4, -2, 0, 6, 12$ a lichá čísla jsou ta, která po dělení dvojkou mají zbytek $1$ tedy $-33, -5, -1, 1, 3, 7, 9$
Vlastnosti sčítání sudých a lichých čísel:
| sudé + sudé = sudé |
| sudé + liché = liché |
| liché + liché = sudé |
Podobná tabulka ale s nasobením:
| sudé $\cdot$ sudé = sudé |
| sudé $\cdot$ liché = sudé |
| liché $\cdot$ liché = liché |
Racionalní a iracionalní čísla:
Racionalní čísla:
- Tuto množinu značíme pomocí písmene Q nebo $\mathbb{Q}$
- Jsou nekonečná spočetná množina čísel
- Vyjadřují se jako zlomek, tedy podíl dvou celých čísel
- Zapisují se většinou $\frac{a}{b}$ nebo $a/b$
- $b \neq 0$
- Desetinný rozvoj racionálního čísla je periodický
- V případě konečného rozvoje tvoří periodu nuly
- Např. $68.24, -9, 3.58, 6.\overline{6}, \frac{22}{7},$ …
Periodický zápis:
V příkladě máme číslo $0.\overline{6}$ neboli $0.6666…$ jedná se o desetiné vyjadření zlomku $\frac{2}{3}$. Je to číslo s nekonečným desetiným rozvojem, ale i tak je racionalní, protože jeho rozvoj je periodický. Periodický rozvoj znamená že se od jisté časti čísla opakuje stejná sekvence čísel. V tomhle připadě to bude do nekonečna se opakujicí $6$. Muže se opakovat do nekonečna i sekvence čísel, např. %123%.
Perioda se značí buď pomocí tří teček nebo, častěji, pomocí čáry nad čísly, která se periodicky opakují. Perioda může začít hned na začátku desetinné části nebo kdykoliv později. Tady jsou různé periodické čísla:
$\frac{2}{3} = 0.666666… = 0.\overline{6}$
$\frac{16}{11} = 1.454545… = 1.\overline{45}$
$\frac{11}{6} = 1.833333… = 1.8\overline{3}$
Iracionalní čísla:
- Jsou všechny ostatní čísla, která nejsou racionalní. Tedy všechna s nekonečným, neperiodickým desetiným rozvojem
- Jsou nekonečná nespočetná množina čísel
- Např. $\pi, e, \sqrt{2},\sqrt{3},\varphi,$ …
Reálná čísla:
- Tuto množinu obvykle značíme písmenem R nebo $\mathbb{R}$
- Jsou nekonečná nespočetná množina čísel
- Reálná čísla jsou např. $3 ,-4\pi, 6.\overline{6}, -9, 68.24, \frac{4}{7}, $ …
- Na reálná čísla můžeme používat všechny základní operace jako: sčítání, odečítání, násobení a dělení.
- Každé nezáporné reálné číslo má druhou odmocninu, které je také reálné číslo. Naopak, žádné záporné reálné číslo nemá jako druhou odmocninu reálné číslo
Reálná čísla obsahují všechna přirozená čísla, celá čísla, racionální čísla a iracionální čísla, proto kdyby jsme si představili nekonečnou číselnou osu, pak reálná čísla představují všechny možné vzdálenosti mezi dvěma body které můžeme na ose nalézt.
Komplexní čísla:
Po reálných číslech následují komplexní čísla. Značí se $\mathbb{C}$. V nich můžeme např. dělit nulou, odmocňovat záporná čísla atd. Komplexní číslo je číslo ve tvaru $a+bi$, kde realné číslo $a$ představuje reálnou část a reálné číslo $b$ imaginární část a $i$ je imaginární jednotka. Pokud je reálná část nulová, jedná se o ryze imaginární komplexní číslo.
Podrobněji budou rozebrána v jednom z budoucích článků, nebo se můžete dočíst více zde.


Napsat komentář