Elektrické pole

1.1 Nabitá tělesa vytvářejí kolem sebe elektrické pole a tím svojí přítomností ovlivňují vlastnosti okolního prostoru. Pokud se do takového pole dostane jiné nabité těleso nebo nabitá částice, bude na ni působit elektrická síla. Elektrické pole má silové účinky. Dále zprostředkovává působení mezi náboji na dálku.

1.2 Jak takové elektrické pole může vypadat? Třeba nějak takto:

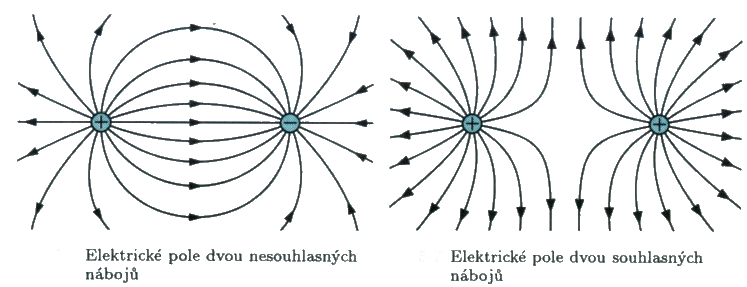
Na obrázku vidíme el. pole dvou dvojic nábojů:

Kladného a záporného – můžeme vidět, že objekty, které mají opačné náboje se přitahují
Kladného a kladného – zde vidíme, že se dva stejné náboje odpuzují

Dále vidíme siločáry. Ty vyobrazují cestu, po které by testovací náboj cestoval, kdyby se na ní nacházel.

1.3 Rozlišujeme mezi homogenním a nehomogenním polem:

Homogenní¹ pole je pole, které má siločáry paralelně² a ve stejné hustotě³. Homogenní pole je například mezi rovnoběžnými deskami kondenzátoru, pokud je odstup mezi deskami malý.
Nehomogenní⁴ pole je tam, kde čáry neprobíhají paralelně a vzdálenost mezi siločárami je rozdílná.

2.1 Aby jsme lépe pochopili elektrické pole, můžeme si ho přirovnat k něčemu co už známe, a to je pole gravitační. Na obrázku můžeme vidět el. pole dvou nábojů, jednoho kladného a jednoho záporného. Pod ním je přirovnání⁵ ke gravitačnímu poli.

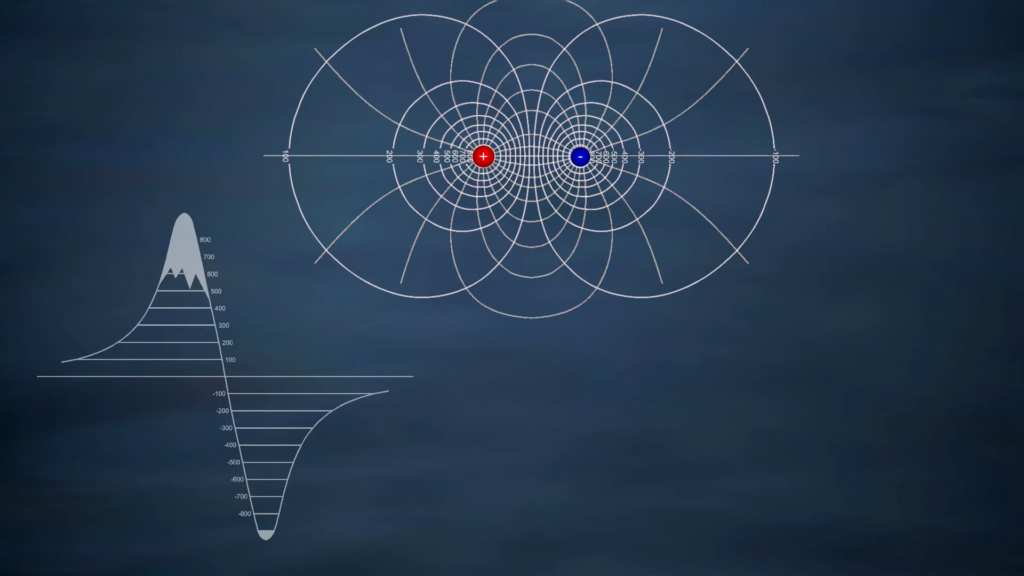
2.2 Můžeme zkusit přidat do pole na předchozím obrázku testovací náboj. Pokud by jsme přidali kladný testovací náboj mezi kladný a záporný náboj tak by cestoval směrem k zápornému náboji stejně jako kdyby jste dali kuličku na vrch té hory. Kulička by spadla až dolů do té propasti.

2.3 Na následujícím obrázku můžete vidět el. pole dvou kladně nabitých nábojů. Kdyby jsme vložili testovací náboj přesně mezi tyhle dva kladné náboje, nic by se nestalo protože se vzájemné působení nábojů ruší. Něco jako kdyby jste položili kuličku mezi tyhle dvě vyobrazené hory.

Takto to zní asi složitě, ale v principu je to jednoduché. Pokud to stále nechápete, doporučuji se podívat na toto video, z animace to jde pochopit lépe.

3.1 Dále bych chtěl říct něco o intenzitě elektrického pole⁶. Veličinu značíme velkým E. Její jednotkou je newton na coulomb $(N/C)$ anebo volt na metr $(V/m)$. Jednotky jsou to v podstatě stejné⁷.

3.2 Co nám tahle veličina vlastně říká? Intenzita elektrického pole je vektorová fyzikální veličina, co vyjadřuje velikost a směr elektrického pole. Je definována jako elektrická síla $F$ působící na těleso s kladným elektrickým nábojem $Q$:

$\displaystyle E = \frac{F}{Q} $

3.3 Orientace Elektrické intenzity je dána domluvou, že zkušebním tělesem je kladně nabité těleso, a tedy elektrická intenzita směřuje od tělesa s kladným elektrickým nábojem k tělesu se záporným elektrickým nábojem.

4.1 Dále tu máme práci v elektrickém poli. Práce v elektrickém poli je ekvivalentní k práci v jiných fyzikálních polích. Můžeme si ji přirovnat k práci v poli gravitačním. Naše gravitační pole je sice trošku nudné a pro naše účely můžeme říct že je homogenní, ale i tak to bude na začátek dobré přirovnání. Vzorec pro potencionální energii tíhovou⁸ je docela známý a jednoduchý. Vzorec vypadá takhle:

$Ep = mgh$

kde $m$ je hmotnost, $g$ tíhové zrychlení a $h$ je výška nad úrovní, pro kterou je potencilální energie nulová (většinou zemský povrh).

4.2 Tíhové zrychlení $g$ naší země nahradíme intenzitou elektrického pole $E$, hmotnost $m$ nahradíme nábojem $Q$⁹ a $h$ nahradíme délkou $l$.

$W = E\cdot Q\cdot l$¹⁰

4.3 Elementární práci elektrického pole vykonanou na přemístění náboje $ q $ po dráze která má délku $ l $ můžeme vyádřit také tímto vzorcem který je v podstatě stejný jako ten předchozí.

$W = F\cdot l$

Což některým může připomenout práci mechanickou a ano ten vzorec je v podstatě stejný, je to $W = F\cdot s$. Za $F$ můžeme dát $q\cdot E$. Rovnost $F = q\cdot E$ můžeme dokázat zase snadno, pomocí toho že rozebereme tyhle odvozené SI jednotky na základní SI jednotky. Veličina $q$ má jednotku coulomb $(C)$¹¹ který lze vyjádřit v základních SI jednotkách jako $s\cdot A$ a veličina $E$ má jednotku volt na metr¹² $(V/m)$. Volt na metr můžeme vyjádřit jako $m\cdot kg\cdot s^{-3}\cdot A^{-1}$¹³. Ještě tam máme $F$, což je síla a ta má jednotku $N$ neboli newton. V základních SI jednotkách to je $m\cdot kg\cdot s^{-2}$. Dáme to pod sebe aby to bylo trošku přehlednější.

$q\cdot E = F$

$(s\cdot A )\cdot (m\cdot kg\cdot s^{-3}\cdot A^{-1}) = m\cdot kg\cdot s^{-2}$

Teď je trochu pokrátíme, můžeme zkrátit $A$ a $A^{-1}$, což se rovná jedna. Zbývá nám tohle:

$(s)\cdot (m\cdot kg\cdot s^{-3}) = m\cdot kg\cdot s^{-2}$

Dále tam máme $s\cdot s^{-3}$ což se rovná $s^{-2}$. a tu už to vidíme jasně:

$m\cdot kg\cdot s^{-2} = m\cdot kg\cdot s^{-2}$

5.1 Pokud to nejde pochopit takhle, ještě by to šlo pochopit kdy si nastudujeme Lorentzovu sílu.

Lorentzova síla je síla pojmenována po Hendriku Antoonovi Lorentzovi, působí na náboj (příp. vodič) v elektromagnetickém poli. Vzorec vypadá následovně. Platí že $F$ je síla, $q$ elektrický náboj, $v$ rychlost náboje, $E$ intenzita elektrického pole, $B$ magnetická indukce a $\times$ vektorový součin.

$\mathbf{F}=q \left(\mathbf{E} + \mathbf{v} \times \mathbf{B}\right)$

5.2 Běžně je jako Lorentzova síla označován pouze příspěvek magnetické síly, tzn.

$\boldsymbol{F}_{\mathrm{mag}} = q \ (\boldsymbol v \times \boldsymbol B)$

5.3 Pokud by jsme zanedbali i příspěvek elektrické síly bude vypadat následovně.

$\boldsymbol{F}_{\mathrm{el}}=q \ \boldsymbol{E}$

6.1 Dále tu ještě máme Coulombův zákon¹⁴. Ten vyjadřuje velikost síly působící mezi dvěma bodovými náboji. Síla $F$ mezi dvěma bodovými náboji $Q_1$ $Q_2$ v klidu je přímo úměrná součinu velikostí nábojů a nepřímo úměrná druhé mocnině jejich vzdálenosti $r$. Ve vzorci pro $F_e$ musíme vzít absolutní hodnotu ze součinu nábojů, neboť velikost elektrické síly $F_e$ je vždy kladná hodnota.

Coulombův zákon v tomto tvaru platí také pro makroskopická tělesa s kulově symetrickým rozložením náboje a pro tělesa, jejichž rozměry jsou zanedbatelné vzhledem k jejich vzdálenosti.

$|F| = \displaystyle k\frac{\left|q_1 q_2\right|}{r^2}$¹⁵

Kde je:

$F$ elektrická síla v newtonech $(N)$,
$q$ náboj částic v coulombech $(C)$,
$r$ vzdálenost nábojů v metrech $(m)$,
a $k$ je konstanta, kterou si vysvětlíme dále.

6.2 Velikost elektrické síly je ovlivněna také prostředím, v němž se náboje nacházejí. Většinou budete asi počítat částice ve vakuu nebo nabitá tělesa ve vzduchu a to by platilo že $k_e \approx 8.988\times 10^9 N\cdot m^2\cdot C^{-2}$ kde $\varepsilon _0$ je permitivita vakua. Ale může to být i v jiném prostředí, třeba být zalita v plastu. To bude potom $k.$ jiné.

$\displaystyle {\displaystyle k = \frac{1}{4\pi \varepsilon }}$

6.3 Permitivitu $\varepsilon$ vypočítáme součinem $\varepsilon _0$ $\cdot$ $\varepsilon _r$.

$\varepsilon = \varepsilon _0 \cdot \varepsilon _r$

6.4 O permitivitě vakua $\varepsilon _0$ současně platí že $\varepsilon_0 \thickapprox 8,854\,187\,812\,8(13) \cdot 10^{-12} \,\,\mathrm{F\cdot m^{-1}}.$ Nebo to můžeme vyjádřit následujím vzorcem kde $c$ je definovaná hodnota rychlosti světla v klasickém vakuu v jednotkách SI a $\mu _0$ je magnetická permeabilita vakua neboli magnetická konstanta. Její aktuální doporučovaná hodnota je $\mu_0 = 1{,}256\,637\,062\,12(19) \cdot 10^{-6}\,\, \mathrm{N\cdot A^{-2}}$ neboli $\mu_0 = 4 \mathrm{\pi} \cdot 10^{-7} \,\,\mathrm{H\cdot m^{-1}}$. Newton na čtvereční ampér ($N/A^2$) je stejný jako henry na metr ($H/m$)¹⁶, v základních SI jednotkách to je $\mathrm{kg\cdot m \cdot A^{-2}\cdot s^{-2}}$.

$\displaystyle \varepsilon _0={\frac {1}{\mu _0c^{2}}}$

A $\varepsilon _r$ a ta nám říká kolikrát je permitivita daného prostředí větší než permitivita vakua. Napříkla $\varepsilon _r$ vody při 0 °C je ~88.

6.5 Takže to můžeme všechno spojit a vyjádřit takhle:

$|F| = \displaystyle \frac{\left|q_1 q_2\right|}{4\pi\varepsilon _0\cdot \varepsilon_k r^2}$

Stejnorodé, rovnoměrně rozložené ↩︎
Tzn. rovnoběžně ↩︎
Neboli ve stejné vzdálenosti od sebe. ↩︎
Tzn. nestejnorodé ↩︎
Je to jen přirovnání a občas může být zavádějící, ale pro naše účely poslouží dobře. ↩︎
též elektrická intenzita ↩︎
Ověřit si to můžete v převodníku. ↩︎
Pokud můžeme silové působení popsat homogenním tíhovým polem s tíhovým zrychlením $g$ (tedy v přiblížení, kdy zanedbáváme pokles tíhového zrychlení s výškou), lze potenciální energii tělesa s hmotností $m$ vyjádřit jednoduchým vztahem $Ep = mgh$ ↩︎
Tady se musím omluvit, myslím že tam má být malé q, ale pokud tam má být velké tak se omlouvám. Každopádně v tom až zas tak velký rozdíl není, více se může dozvědět zde. ↩︎
Pomocí tohohle vzorce je definováno elektrické napětí. ↩︎
Velikost coulombu i ampéru je definovaná fixací číselné hodnoty velikosti elementárního náboje e : $e = 1.602 176 634 \times 10^{-19} C$ (přesně). Náboj protonu je $e$, náboj elektronu je přesně opačný, $-e = -1.602 176 634 \times 10^{-19} C$. ↩︎
Nebo newton na coulomb $(N/C)$ viz odstavec 3.1. ↩︎
Zdroj 7. ↩︎
Coulombův zákon tu nebudu brát pouze pro tělesa ve vakuu, ale pokusím se tu vysvětlit jak to funguje když se nenachází ve vakuu. ↩︎
Můžete si všimnout podobnosti s Newtonovým gravitačním zákonem který vypadá takhle: $F_g = G \displaystyle{\frac{ m_1 m_2}{r^2}}$ ↩︎
viz. převodník ↩︎

Zdroje:

Elektrické pole

Komentáře

Napsat komentář Zrušit odpověď na komentář