Osnova:
1.1 Druhy čísel:
Jaké jsou druhy čísel? Máme tu přirozená čísla která obsahují jen kladná čísla. Celá čísla která obsahují kladná i záporná čísla. Racionální čísla jsou všechny zlomky. Iracionální čísla jsou čísla s nekonečným, neperiodickým počtem desetinných míst. Reálná čísla obsahují všechna racionální a iracionální čísla. Komplexní čísla jsou nadstavbou nad reálná kvůli např. odmocninám se záporným číslem.
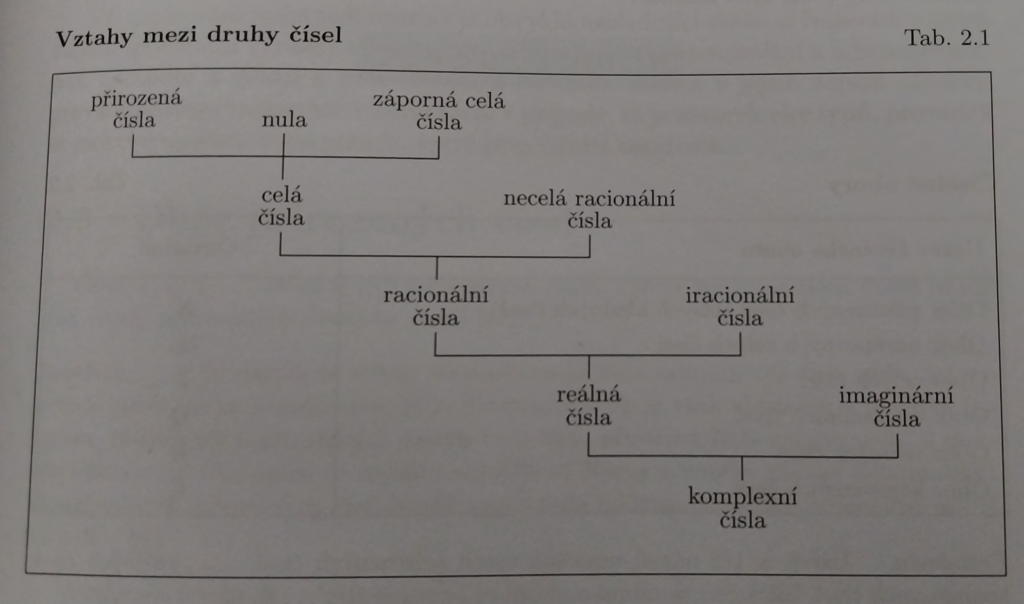
Zdroj obrázku je z knihy: Přehled středoškolské matematiky – Jozef Polák
Více informací o tomto tématu najdete zde.
1.2 Dělitelnost přirozených čísel:
| 1 | Jedničkou je dělitelné každé přirozené číslo |
| 2 | Dvojkou je dělitelné každé sudé číslo (končící 0, 2, 4, 6, 8) |
| 3 | Ciferný součet čísla je dělitelný třemi. Příklad: 2625 ⇒ 2 + 6 + 2 + 5 = 15 ⇒ ANO 7243 ⇒ 7 + 2 + 4 + 3 = 16 ⇒ NE |
| 4 | Poslední dvojčíslí je dělitelné čtyřmi. |
| 5 | Číslo končí 0 nebo 5. |
| 6 | Číslo je dělitelné dvěma a současně třemi. Tedy sudé číslo, jehož ciferný součet je dělitelný třemi. |
| 7 | Poslední číslice se vynásobí dvěma a odečte se od zbytku čísla (daného čísla bez poslední číslice). Výsledek musí být dělitelný sedmi. Postup lze opakovat, dokud se nedosáhne nízkého čísla. Příklad: 154 ⇒ 15 – 2 · 4 = 7 ⇒ ANO 2982 ⇒ 298 – 2 · 2 = 294 ⇒ 29 – 2 · 4 = 21 ⇒ ANO 243 ⇒ 24 – 2 · 3 = 18 ⇒ NE |
| 8 | Poslední trojčíslí je dělitelné osmi. |
| 9 | Ciferný součet čísla je dělitelný devíti. |
| 10 | Končí číslicí 0. |
| 11 | Číslice na sudých místech se přičítají a číslice na lichých místech se odečítají. Lze postupovat i opačným způsobem. Výsledek musí být dělitelný jedenácti. Příklad: 3927 ⇒ 3 – 9 + 2 – 7 = –11 ⇒ ANO; nebo 3927 ⇒ –3 + 9 – 2 + 7 = 11 ⇒ ANO 2824 ⇒ 2 – 8 + 2 – 4 = –8 ⇒ NE |
| 12 | Číslo je dělitelné třemi a zároveň čtyřmi. |
| 13 | Sečtou se trojčíslí na sudých místech a odečtou se trojčíslí na lichých místech. |
| 14 | Číslo je dělitelné dvěma a zároveň sedmi. |
| 15 | Číslo dělitelné pěti a zároveň třemi. |
| 20 | Poslední dvojčíslí je dělitelné dvaceti. Končí dvojčíslím 00, 20, 40, 60, 80 |
| 25 | Poslední dvojčíslí je dělitelné dvacetipěti. Končí dvojčíslím 00, 25, 50 nebo 75. |
| 50 | Poslední dvojčíslí je dělitelné padesáti Končí dvojčíslím 00 nebo 50. |
1.3 Celá čísla, racionální čísla, reálná čísla:
Více buď výše v článku nebo v dalším článku kde jsem to rozebral celé.
1.4 Absolutní hodnota reálného čísla:
- Vyjadřuje vzdálenost na číselné ose od nuly.
- Značí se dvěma svislými čarami $|x|$
- Je to vždy kladné číslo neboli větší nebo rovno nule.
- Absolutní hodnota kladného čísla je stejné číslo ($|x|=x$; např. $|4|=4$)
- Absolutní hodnota z čísla záporného je číslo opačné $|-x|=x$
Definice absolutní hodnoty reálného čísla $a$:
$|a| = \left\{ \begin{array}{rcl} a & \mbox{ pokud } a\geq0 \\ -a & \mbox{ pokud } a<0 \end{array}\right.$


Napsat komentář